Intermediate Value Theorem Worksheet. Here is the Intermediate Value Theorem stated more formally: When: The curve is the function y = f(x) In this Intermediate Value Theorem worksheet, students identify and explain a continuous function. Introduction to the Intermediate value theorem.
Check out this review article to learn what you need to know for the AP The Intermediate Value Theorem (IVT).
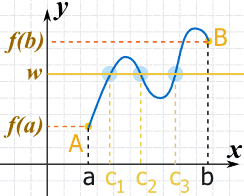
Intermediate Value Theorem. -if f is continuous for all x in interval [a, b] and y is a number between f(a) and f(b), then there's a number x=c in (a, b) for which f(c)=y -basically, if you have a continuous function and you pick a number on the y-axis in an interval, there's a. corresponding x-value in that interval.
Lesson: Intermediate Value Theorem | Nagwa
Intermediate value theorem - Wikipedia
Intermediate Value Theorem: Definition, Examples ...
Intermediate Value Theorem: Examples and Applications ...
Pin by Teacher's Notebook on 9th -12th Grade | Pinterest
Intermediate Value Theorem
ShowMe - intermediate value theorem
Intermediate Value Theorem Explained - To Find Zeros ...
Answered: Use the intermediate value theorem to… | bartleby
Here's the statement of the theorem: Suppose f is a function that is continuous on the closed interval [a, b]. The Intermediate Value Theorem is one of the most important theorems in Introductory Calculus, and it forms the basis for proofs of many results in subsequent and advanced Mathematics courses. In mathematical analysis, the intermediate value theorem states that if f is a continuous function whose domain contains the interval [a, b], then it takes on any given value between f(a) and f(b).
